日常生活中衣、食、住、行等诸多方面均与数学密切相关,如牙膏、饼干、瓜子等大小包装与其价格之间的关系;吃东西时营养成分的搭配;电灯的位置与照明度的关系;窗户的面积与采光量的关系等等.我们通过分析和归纳,把这些司空见惯的普遍现象和普通问题抽象为数学问题,找出常量、变量与函数关系.建立数学模型,能够求解出我们需要的答案.
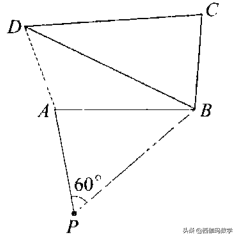
例1如图,某海滨在P处有--沙堆,经清洁之后,今要把这堆沙送到海滩△BCD中去.已知PA=100 m,PB=150 m,∠APB=60° .能否在海滩中确定出一条界线,使位于界线一侧的沿道路PA送沙较近,而另一侧的沿道路PB送沙较近?如果能,请说出这条界线是一 条什么曲线.
例2 有两种海产品甲和乙,其价格分别为每千克33元和24元.每种海产品包含三种营养物,但数量不同,列表如下:
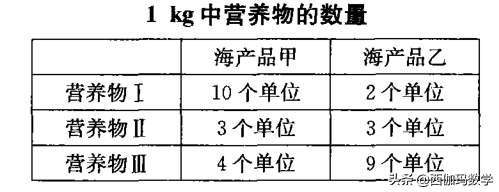
某种食品中需要得到的营养物的数量如下:
营养物I :至少20个单位;营养物I :至少18个单位;营养物皿:至少36个单位.
在保证营养符合标准的条件下,需要甲和乙各多少千克,才能使费用最小?
例3某个码头上起吊245桶液体原料,因是同型圆柱桶装运,故起吊时堆放以等腰梯形为宜,且上下层只相差一桶. 在不考虑占地面积、堆放高度与重压时,堆放方案有哪几种?
例4 某山村有荒山若干亩,为了改善生态环境,用飞机播种种草养殖大山羊.第1年生草量10万kg.如果年新生草量不超过420万kg,那么每年新生草量将以200%的增长率递增(旧草自然枯竭、落种);若超过此量,草地有荒废的危险.每只大山羊平均年食草量为500 kg. 该山村从第2年起年养殖大山羊保持在200只.
(1)写出年新生草量y与年份n的函数关系.
(2)第几年后应将养殖的大山羊总数增加到最大数量?最大数量为多少只?
例5 年初某下岗职工承包了一个商店,元月初向银行贷款10 000 元作为进货资金.每月月底可售出全部货物,获得毛利(当月销售收入与投入资金之差)是该月月初投入20%.每月月底需支出税款等费用共占该月毛利的60%.此外,该职工每月还要支出生活费300元.余款作为下月投入资金用于进货.如此继续下去,年底该职工拥有多少资金?若贷款年利率为5.72% ,该职工的纯收入为多少? (1. 08^11≈2.3316,结果保留整数)
1
问:车轮为什么都是圆的,而不是其他形状?
答:同学们都知道,圆上任何一点到圆心的距离都是相等的。把车轮做成圆形,车轴在圆心上,当车轮在地面滚动时,车轴离地面的距离,总是等于车轮半径。车里坐的人,就能平稳地被车子拉着走。
反之,如果车轮设计成三角形或是正方形,一定会颠簸得要命。
把车轮做成圆形还有一大好处:当一样东西在地上滚动的时候,要比拖着走省劲多了,这是滚动摩擦阻力比滑动摩擦阻力小的缘故。
2
问:除了圆形井盖,为什么很少见到其他形状的井盖?
答:同一个圆内的直径都相等,只要井盖直径大于窨井口,那么不论怎样移动它都不会掉下去,这样就有安全保障了。
如果设计成三角形或正方形的,即使比窨井口大一些,但还是有掉下去的可能。
由于窨井有时需要人工清理或架线,所以要求其面积尽可能地大。而在各种几何图形中,周长相等时,只有圆形的面积最大,同时没有易使人受伤的角和尖。
除了安全以外,另一个好处就是圆形便于运输。
3
问:四叶草为什么又叫“幸运草”?

答:四叶草,学名苜蓿草,是多年生草本植物。一般只有三片小叶子,叶呈心形,叶心较深色的部分亦是心形。
四叶草是由三叶草基因突变而产生的,它只占其中的10万分之一。也就说在10万株苜蓿草中,你可能只会发现一株是四叶的。因为机率太小,因此四叶草被国际公认为幸运的象征。
4
问:风扇的叶片为什么都是奇数,而不是偶数?
答:如果叶片数量为偶数设计,形成对称的排列方式,不但使得风扇自身的平衡性难以调整,而且容易使风扇在高速运转时产生更多的共振,从而导致叶片无法长时间承受共振产生的疲劳,最终出现断裂等情况。
因此,轴流风扇的设计多为不对称的奇数叶片设计。同样的理念,在螺旋桨直升飞机的设计中也有体现。
5
问:猫和狗在冬天睡觉时,为什么总是把身体蜷成球形?
答:数学上,在体积一定的情况下,表面积最小的物体是球体。
缩成一个球体,可以减小和外界接触的面积,降低热交换的速度,减少身体内热量散发的速度,节省能量,保持体温。
6
问:看看下面带箭头的两条线段,猜猜哪条更长?
答:这就是有名的“缪勒莱耶错觉”,也叫箭形错觉。一条线段的两端加上向外的两条斜线,另一条线段则加上向内的两条斜线,则前者要显得比后者长得多。
对于这种错觉有一种理论,叫神经抑制作用理论,它认为当两个轮廓彼此贴近时,视网膜上相邻的神经团会相互抑制,结果轮廓发生位移,产生了错觉。
7
问:我们常说“天有不测风云”,为什么天气预报有时会出错?
答:这涉及一个数学定义——“混沌”,即“初始值的极端不稳定性”。
在正常情况下,天气模式基本上遵循着合理进程,通过若干种不同的模拟方式,就能推测未来的天气变化。
然而,天气是由一系列复杂因素组合而成的。初始条件的微小变化会使预报结果差异很大,这时天气已经进入了混沌区域,预报的时间越长,到达混沌点的可能性就越大,准确率就越不好把握。
8问:黄金分割为什么是0.618?答:0.618,一个极为迷人而神秘的数字,也被称为黄金分割律,它是古希腊著名数学家毕达哥拉斯于2500多年前发现的。有一次,毕达哥拉斯路过铁匠作坊,被叮叮当当的打铁声迷住了。为了揭开这清脆悦耳的声音中隐藏的秘密,他测量了铁锤和铁砧的尺寸,发现它们之间存在着十分和谐的比例关系。回到家里,他又取出一根线,分为两段,反复比较,最后认定1∶0.618的比例最为优美。此后,这个数字一直被奉为科学和美学的金科玉律。音乐会上,报幕员的最佳位置,是舞台宽度的0.618之处;二胡要获得最佳音色,其“千斤”(对琴弦起固定和切弦作用的部件)须放在琴弦长度的0.618处;埃菲尔铁塔也是黄金比例建筑的典范……

